How To Find Minimum Speed In Projectile Motion

19 3.four Projectile Move

Summary

Identify and explain the properties of a projectile, such as acceleration due to gravity, range, maximum height, and trajectory.
Determine the location and velocity of a projectile at different points in its trajectory.
Apply the principle of independence of motion to solve projectile movement bug.

Projectile motion is the motion of an object thrown or projected into the air, bailiwick to but the acceleration of gravity. The object is called a projectile , and its path is called its trajectory . The movement of falling objects, every bit covered in Chapter ii.6 Trouble-Solving Basics for One-Dimensional Kinematics, is a simple one-dimensional type of projectile motion in which there is no horizontal motion. In this section, nosotros consider ii-dimensional projectile motility, such as that of a football game or other object for which air resistance is negligible .

The almost of import fact to recollect here is that motions forth perpendicular axes are independent and thus tin be analyzed separately. This fact was discussed in Chapter 3.1 Kinematics in Two Dimensions: An Introduction, where vertical and horizontal motions were seen to be independent. The key to analyzing two-dimensional projectile motion is to break it into ii motions, one along the horizontal axis and the other along the vertical. (This choice of axes is the most sensible, because acceleration due to gravity is vertical—thus, in that location will exist no acceleration along the horizontal axis when air resistance is negligible.) As is customary, we phone call the horizontal axis the x -axis and the vertical axis the y -centrality. Figure ane illustrates the notation for deportation, where $\textbf{s}$ is defined to be the total displacement and $\textbf{x}$ and $\textbf{y}$ are its components along the horizontal and vertical axes, respectively. The magnitudes of these vectors are southward , x , and y . (Note that in the last section we used the note $\textbf{A}$ to represent a vector with components $\boldsymbol{\textbf{A}_x}$ and $\boldsymbol{\textbf{A}_y}.$ If we connected this format, we would call displacement $\textbf{s}$ with components $\boldsymbol{\textbf{s}_x}$ and $\boldsymbol{\textbf{s}_y}.$ However, to simplify the notation, we volition simply represent the component vectors every bit $\textbf{x}$ and $\textbf{y}$ .)

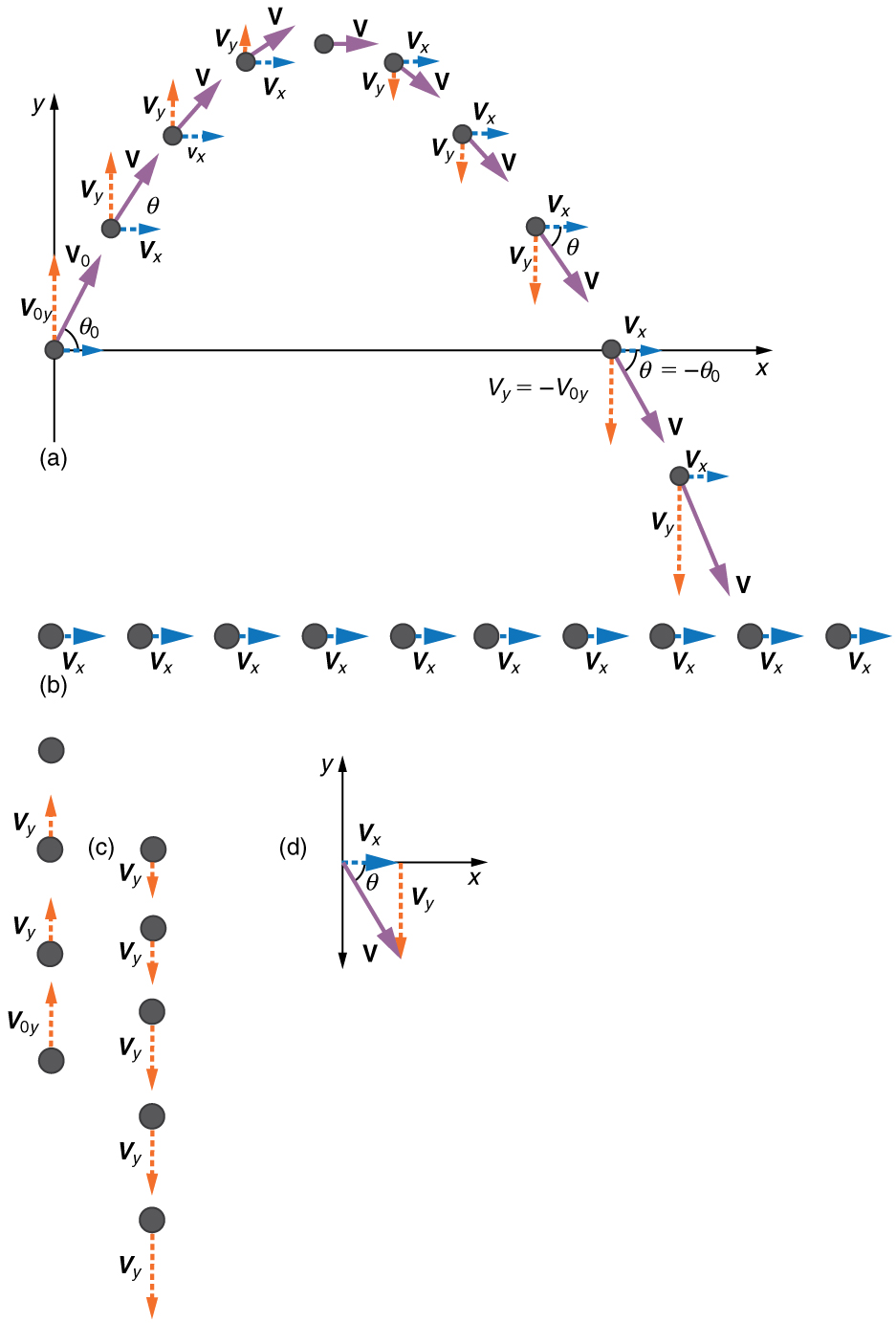
Of class, to draw motion we must deal with velocity and dispatch, as well as with deportation. We must observe their components along the 10 – and y -axes, as well. We will presume all forces except gravity (such equally air resistance and friction, for example) are negligible. The components of dispatch are then very uncomplicated: $\boldsymbol{\textbf{a}_y=-g=-9.80\textbf{ m/s}^2}.$ (Note that this definition assumes that the upwards management is defined equally the positive management. If you suit the coordinate arrangement instead such that the downwards direction is positive, then acceleration due to gravity takes a positive value.) Because gravity is vertical, $\boldsymbol{\textbf{a}_x=0}.$ Both accelerations are abiding, and so the kinematic equations tin can be used.

REVIEW OF KINEMATIC EQUATIONS (Abiding α)

$\boldsymbol{x=x_0+\bar{v}t}$

$\boldsymbol{\bar{v}=}$ $\boldsymbol{\frac{v_0+v}{2}}$

$\boldsymbol{v=v_0+at}$

$\boldsymbol{x=x_0+v_0t\:+}$ $\boldsymbol{\frac{1}{2}}$ $\boldsymbol{at^2}$

$\boldsymbol{v_2=v_0^2+2a(x-x_0).}$

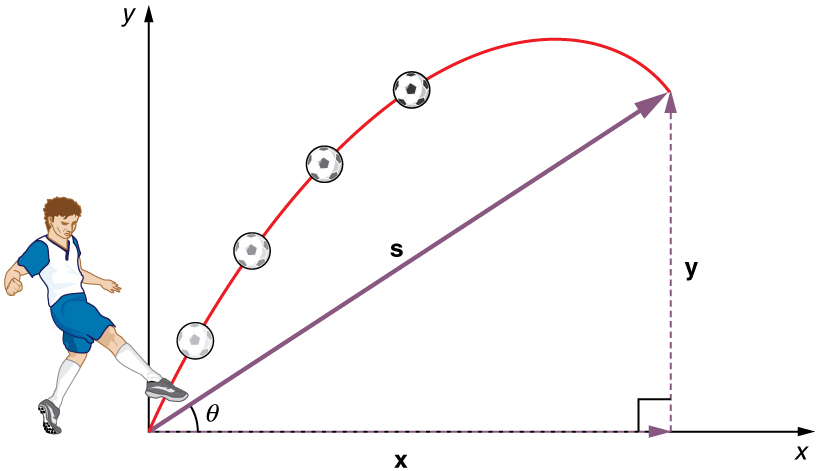
A soccer player is kicking a soccer ball. The ball travels in a projectile motion and reaches a point whose vertical distance is y and horizontal distance is x. The displacement between the kicking point and the final point is s. The angle made by this displacement vector with x axis is theta.

Given these assumptions, the following steps are and so used to clarify projectile motility:

Step 1. Resolve or break the movement into horizontal and vertical components along the ten- and y-axes. These axes are perpendicular, so $\boldsymbol{\textbf{A}_x=\textbf{A cos}\:\theta}$ and $\boldsymbol{\textbf{A}_y=\textbf{A sin}\:\theta}$ are used. The magnitude of the components of deportation $\textbf{s}$ along these axes are $\boldsymbol{x}$ and $\boldsymbol{y}.$ The magnitudes of the components of the velocity $\textbf{v}$ are $\boldsymbol{v_x=v\textbf{cos}\theta}$ and $\boldsymbol{v_y=v\textbf{sin}\theta},$ where $\boldsymbol{v}$ is the magnitude of the velocity and $\boldsymbol{\theta}$ is its direction, as shown in Figure two. Initial values are denoted with a subscript 0, as usual.

Stride 2. Treat the motility as two contained one-dimensional motions, one horizontal and the other vertical. The kinematic equations for horizontal and vertical motility take the following forms:

$\boldsymbol{\textbf{Horizontal Motion}(a_x=0)}$

$\boldsymbol{x=x_0+v_xt}$

$\boldsymbol{v_x=v_{0x}=v_x=\textbf{velocity is a constant.}}$

$\boldsymbol{\textbf{Vertical Motion(assuming positive is up} \; a_y=-g=-9.80\textbf{ m/s}^2)}$

$\boldsymbol{y=y_0\:+}$ $\boldsymbol{\frac{1}{2}}$ $\boldsymbol{(v_{0y}+v_y)t}$

$\boldsymbol{v_y=v_{0y}-gt}$

$\boldsymbol{y=y_0+v_{0y}t\:-}$ $\boldsymbol{\frac{1}{2}}$ $\boldsymbol{gt^2}$

$\boldsymbol{v_y^2=v_{0y}^2-2g(y-y_0).}$

Stride iii. Solve for the unknowns in the two separate motions—1 horizontal and one vertical. Annotation that the simply mutual variable between the motions is time $\boldsymbol{t}.$ The trouble solving procedures here are the same as for i-dimensional kinematics and are illustrated in the solved examples below.

Step 4. Recombine the ii motions to find the total displacement $\textbf{s}$ and velocity $\textbf{v}.$ Considering the x – and y -motions are perpendicular, we determine these vectors past using the techniques outlined in the Chapter 3.three Vector Addition and Subtraction: Belittling Methods and employing $\boldsymbol{\textbf{A}=\sqrt{\textbf{A}_x^2+\textbf{A}_y^2}}$ and $\boldsymbol{\theta=\textbf{tan}^{-1}(\textbf{A}_y\:/\:\textbf{A}_x)}$ in the post-obit form, where $\boldsymbol{\theta}$ is the direction of the displacement $\textbf{s}$ and $\boldsymbol{\theta_v}$ is the direction of the velocity $\textbf{v}:$

Full displacement and velocity

$\boldsymbol{s=\sqrt{x^2+y^2}}$

$\boldsymbol{\theta=\textbf{tan}^{-1}(y/x)}$

$\boldsymbol{v=\sqrt{v_x^2+v_y^2}}$

$\boldsymbol{\theta_{v}=\textbf{tan}^{-1}(v_y\:/\:v_x).}$

In part a the figure shows projectile motion of a ball with initial velocity of v zero at an angle of theta zero with the horizontal x axis. The horizontal component v x and the vertical component v y at various positions of ball in the projectile path is shown. In part b only the horizontal velocity component v sub x is shown whose magnitude is constant at various positions in the path. In part c only vertical velocity component v sub y is shown. The vertical velocity component v sub y is upwards till it reaches the maximum point and then its direction changes to downwards. In part d resultant v of horizontal velocity component v sub x and downward vertical velocity component v sub y is found which makes an angle theta with the horizontal x axis. The direction of resultant velocity v is towards south east. — **Effigy 2.** (a) We analyze two-dimensional projectile motion by breaking information technology into ii independent one-dimensional motions along the vertical and horizontal axes. (b) The horizontal movement is simple, because *a_x* =0 and *5_x* is thus constant. (c) The velocity in the vertical direction begins to decrease as the object rises; at its highest point, the vertical velocity is cypher. As the object falls towards the Earth again, the vertical velocity increases over again in magnitude but points in the opposite direction to the initial vertical velocity. (d) The 10 – and y -motions are recombined to requite the total velocity at whatever given bespeak on the trajectory.

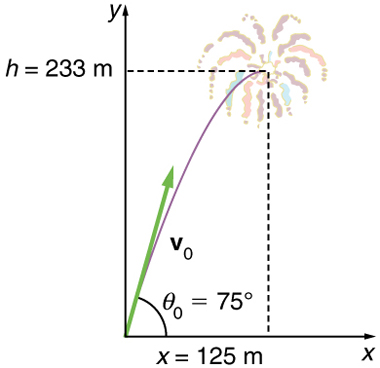
Example 1: A Fireworks Projectile Explodes High and Away

During a fireworks display, a shell is shot into the air with an initial speed of 70.0 m/s at an angle of $\boldsymbol{75.0^o}$ to a higher place the horizontal, as illustrated in Effigy 3. The fuse is timed to ignite the shell simply as it reaches its highest point above the footing. (a) Summate the height at which the crush explodes. (b) How much time passed between the launch of the trounce and the explosion? (c) What is the horizontal displacement of the crush when it explodes?

Strategy

Because air resistance is negligible for the unexploded shell, the analysis method outlined above can be used. The motion can be cleaved into horizontal and vertical motions in which $\boldsymbol{a_x=0}$ and $\boldsymbol{a_y=-g}.$ We can so define $\boldsymbol{x_0}$ and $\boldsymbol{y_0}$ to exist zero and solve for the desired quantities.

Solution for (a)

By "height" we mean the altitude or vertical position $\boldsymbol{y}$ above the starting point. The highest point in any trajectory, called the apex, is reached when $\boldsymbol{v_y=0}.$ Since we know the initial and final velocities equally well every bit the initial position, nosotros use the post-obit equation to observe $\boldsymbol{y}:$

$\boldsymbol{v_y^2=v_{0y}^2-2g(y-y_0).}$

The x y graph shows the trajectory of fireworks shell. The initial velocity of the shell v zero is at angle theta zero equal to seventy five degrees with the horizontal x axis. The fuse is set to explode the shell at the highest point of the trajectory which is at a height h equal to two hundred thirty three meters and at a horizontal distance x equal to one hundred twenty five meters from the origin.

Considering $\boldsymbol{y_0}$ and $\boldsymbol{v_y}$ are both nix, the equation simplifies to

$\boldsymbol{0=v_{0y}^2-2gy.}$

Solving for $\boldsymbol{y}$ gives

$\boldsymbol{y\:=}$ $\boldsymbol{\frac{v_{0y}^2}{2g}.}$

Now nosotros must find $\boldsymbol{v_0},$ the component of the initial velocity in the y-direction. Information technology is given past $\boldsymbol{v_{0y}=v_0\:\textbf{sin}\:\theta},$ where $\boldsymbol{v_{0y}}$ is the initial velocity of 70.0 one thousand/south, and $\boldsymbol{\theta_0=75.0^o}$ is the initial angle. Thus,

$\boldsymbol{v_{0y}=v_0\:\textbf{sin}\:\theta_0=(70.0\textbf{ m/s})(\textbf{sin }75^o)=67.6\textbf{ m/s}.}$

and $\boldsymbol{y}$ is

$\boldsymbol{y\:=}$ $\boldsymbol{\frac{(67.6\textbf{ m/s})^2}{2(9.80\textbf{ m/s}^2)}},$

so that

$\boldsymbol{y=233\textbf{ m}.}$

Discussion for (a)

Note that because upwards is positive, the initial velocity is positive, as is the maximum pinnacle, just the acceleration due to gravity is negative. Annotation besides that the maximum acme depends only on the vertical component of the initial velocity, and then that any projectile with a 67.6 1000/due south initial vertical component of velocity will reach a maximum superlative of 233 1000 (neglecting air resistance). The numbers in this instance are reasonable for large fireworks displays, the shells of which exercise reach such heights before exploding. In practice, air resistance is not completely negligible, and so the initial velocity would have to be somewhat larger than that given to achieve the same height.

Solution for (b)

Every bit in many physics bug, at that place is more than one manner to solve for the time to the highest signal. In this case, the easiest method is to use $\boldsymbol{y=y_0+\frac{1}{2}(v_{0y}+v_y)t}.$ Because $\boldsymbol{y_0}$ is zero, this equation reduces to simply

$\boldsymbol{y\:=}$ $\boldsymbol{\frac{1}{2}}$ $\boldsymbol{(v_{0y}+v_y)t.}$

Annotation that the final vertical velocity, $\boldsymbol{v_y},$ at the highest betoken is zero. Thus,

$\boldsymbol{t=\frac{2y}{(v_{0y}+v_y)}=\frac{2(233\textbf{ m})}{(67.6\textbf{ m/s})}}$

$\boldsymbol{=6.90\textbf{ s}.}\:\:\:\:\:\:\:\:\:$

Discussion for (b)

This time is also reasonable for large fireworks. When you lot are able to see the launch of fireworks, yous will discover several seconds pass earlier the trounce explodes. (Another fashion of finding the fourth dimension is by using $\boldsymbol{y=y_0+v_{0y}t-\frac{1}{2}gt^2},$ and solving the quadratic equation for $\boldsymbol{t}$ .)

Solution for (c)

Because air resistance is negligible, $\boldsymbol{a_x=0}$ and the horizontal velocity is constant, equally discussed above. The horizontal deportation is horizontal velocity multiplied by time equally given by $\boldsymbol{x=x_0+v_xt},$ where $\boldsymbol{x_0}$ is equal to zero:

$\boldsymbol{x=v_xt,}$

where $\boldsymbol{v_x}$ is the 10-component of the velocity, which is given past $\boldsymbol{v_x=v_0\textbf{cos}\:\theta_0.}$ Now,

$\boldsymbol{v_x=v_0\textbf{cos}\theta_0=(70.0\textbf{ m/s})(\textbf{cos }75.0^o)=18.1\textbf{ m/s}.}$

The time $\boldsymbol{t}$ for both motions is the same, and so $\boldsymbol{x}$ is

$\boldsymbol{x=(18.1\textbf{ m/s})(6.90\textbf{ s})=125\textbf{ m}.}$

Discussion for (c)

The horizontal motion is a constant velocity in the absenteeism of air resistance. The horizontal deportation establish hither could exist useful in keeping the fireworks fragments from falling on spectators. In one case the vanquish explodes, air resistance has a major effect, and many fragments volition land direct below.

In solving role (a) of the preceding instance, the expression we found for $\boldsymbol{y}$ is valid for whatsoever projectile motion where air resistance is negligible. Call the maximum pinnacle $\boldsymbol{y=h};$ then,

$\boldsymbol{h\:=}$ $\boldsymbol{\frac{v_{0y}^2}{2g}.}$

This equation defines the maximum acme of a projectile and depends only on the vertical component of the initial velocity.

Example two: Computing Projectile Movement: Hot Stone Projectile

Kilauea in Hawaii is the world'due south virtually continuously active volcano. Very active volcanoes characteristically eject red-hot rocks and lava rather than fume and ash. Suppose a large rock is ejected from the volcano with a speed of 25.0 g/s and at an angle $\boldsymbol{35.0^o}$ above the horizontal, as shown in Figure 4. The rock strikes the side of the volcano at an distance 20.0 m lower than its starting bespeak. (a) Summate the time it takes the rock to follow this path. (b) What are the magnitude and direction of the rock's velocity at touch?

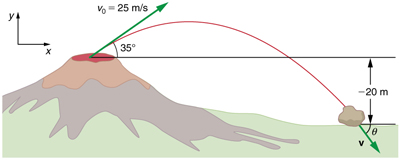
The trajectory of a rock ejected from a volcano is shown. The initial velocity of rock v zero is equal to twenty five meters per second and it makes an angle of thirty five degrees with the horizontal x axis. The figure shows rock falling down a height of twenty meters below the volcano level. The velocity at this point is v which makes an angle of theta with horizontal x axis. The direction of v is south east.

Strategy

Once more, resolving this 2-dimensional move into two independent i-dimensional motions will allow united states to solve for the desired quantities. The time a projectile is in the air is governed by its vertical move lonely. Nosotros will solve for $\boldsymbol{t}$ first. While the rock is rising and falling vertically, the horizontal motion continues at a constant velocity. This case asks for the concluding velocity. Thus, the vertical and horizontal results will be recombined to obtain $\boldsymbol{v}$ and $\boldsymbol{\theta_v}$ at the last time $\boldsymbol{t}$ determined in the first role of the example.

Solution for (a)

While the rock is in the air, it rises and then falls to a concluding position twenty.0 m lower than its starting altitude. We can find the time for this by using

$\boldsymbol{y=y_0+v_{0y}t\:-}$ $\boldsymbol{\frac{1}{2}}$ $\boldsymbol{gt^2.}$

If we take the initial position $\boldsymbol{y_0}$ to be zilch, then the concluding position is $\boldsymbol{y=-20.0\textbf{ m}}.$ Now the initial vertical velocity is the vertical component of the initial velocity, institute from $\boldsymbol{v_{0y}=v_0\:\textbf{sin}\:\theta_0= (25.0\textbf{ m/s})(\textbf{sin }35.0^o)=14.3\textbf{ m/s}}.$ Substituting known values yields

$\boldsymbol{-20.0\textbf{ m}=(14.3\textbf{ m/s})t-4.90\textbf{ m/s}^2t^2.}$

Rearranging terms gives a quadratic equation in $\boldsymbol{t}:$

$\boldsymbol{4.90\textbf{ m/s}^2t^2-14.3\textbf{ m/s}t-20.0\textbf{ m}=0.}$

This expression is a quadratic equation of the grade $\boldsymbol{at^2+bt+c=0},$ where the constants are $\boldsymbol{a=4.90},\boldsymbol{b=-14.3},$ and $\boldsymbol{c=-20.0.}$ Its solutions are given by the quadratic formula:

$\boldsymbol{t\:=}$ $\boldsymbol{\frac{-b\pm\sqrt{b^2-4ac}}{2a}}$

This equation yields 2 solutions: $\boldsymbol{t=3.96}$ and $\boldsymbol{t=-1.03}.$ (It is left as an exercise for the reader to verify these solutions.) The fourth dimension is $\boldsymbol{t=3.96\textbf{ s}}$ or $\boldsymbol{-1.03\textbf{ s}}.$ The negative value of time implies an consequence before the start of movement, and so nosotros discard it. Thus,

$\boldsymbol{t=3.96\textbf{ s}.}$

Discussion for (a)

The time for projectile motion is completely determined by the vertical motion. So any projectile that has an initial vertical velocity of 14.3 chiliad/s and lands xx.0 m below its starting altitude volition spend 3.96 southward in the air.

Solution for (b)

From the data now in mitt, we tin find the terminal horizontal and vertical velocities $\boldsymbol{v_x}$ and $\boldsymbol{v_y}$ and combine them to find the total velocity $\boldsymbol{v}$ and the angle $\boldsymbol{\theta_0}$ it makes with the horizontal. Of course, $\boldsymbol{v_x}$ is constant so we can solve for it at any horizontal location. In this case, we chose the starting point since we know both the initial velocity and initial angle. Therefore:

$\boldsymbol{v_x=v_0\:\textbf{cos}\:\theta_0=(25.0\textbf{ m/s})(\textbf{cos }35^o)=20.5\textbf{ m/s}.}$

The final vertical velocity is given by the following equation:

$\boldsymbol{v_y=v_{0y}-gt,}$

where $\boldsymbol{v_{0y}}$ was constitute in function (a) to be $\boldsymbol{14.3\textbf{ m/s}}.$ Thus,

$\boldsymbol{v_y=14.3\textbf{ m/s}-(9.80\textbf{ m/s}^2)(3.96\textbf{ s})}$

so that

$\boldsymbol{v_y=-24.5\textbf{ m/s}.}$

To find the magnitude of the concluding velocity $\boldsymbol{v}$ we combine its perpendicular components, using the post-obit equation:

$\boldsymbol{v=\sqrt{v_x^2+v_y^2}=\sqrt{(20.5\textbf{ m/s})^2+(-24.5\textbf{ m/s})^2},}$

which gives

$\boldsymbol{v=31.9\textbf{ m/s}.}$

The management $\boldsymbol{\theta_v}$ is plant from the equation:

$\boldsymbol{\theta_v=\textbf{tan}^{-1}(v_y\:/\:v_x)}$

so that

$\boldsymbol{\theta_v=\textbf{tan}^{-1}(-24.5/20.5)=\textbf{tan}^{-1}(-1.19).}$

Thus,

$\boldsymbol{\theta_v=-50.1^o.}$

Give-and-take for (b)

The negative angle ways that the velocity is $\boldsymbol{50.1^o}$ beneath the horizontal. This consequence is consistent with the fact that the final vertical velocity is negative and hence down—as you would expect because the final distance is xx.0 m lower than the initial altitude. (Run across Effigy 4.)

One of the most important things illustrated past projectile movement is that vertical and horizontal motions are contained of each other. Galileo was the first person to fully comprehend this characteristic. He used it to predict the range of a projectile. On level basis, nosotros define range to be the horizontal distance $\textbf{R}$ traveled by a projectile. Galileo and many others were interested in the range of projectiles primarily for military purposes—such equally aiming cannons. However, investigating the range of projectiles can shed light on other interesting phenomena, such as the orbits of satellites around the Earth. Let united states consider projectile range further.

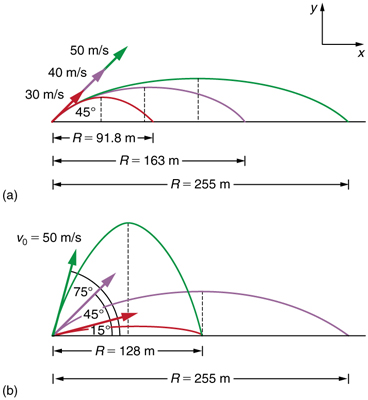
Part a of the figure shows three different trajectories of projectiles on level ground. In each case the projectiles makes an angle of forty five degrees with the horizontal axis. The first projectile of initial velocity thirty meters per second travels a horizontal distance of R equal to ninety one point eight meters. The second projectile of initial velocity forty meters per second travels a horizontal distance of R equal to one hundred sixty three meters. The third projectile of initial velocity fifty meters per second travels a horizontal distance of R equal to two hundred fifty five meters.

How does the initial velocity of a projectile bear on its range? Obviously, the greater the initial speed $\boldsymbol{v_0},$ the greater the range, as shown in Figure 5(a). The initial bending $\boldsymbol{\theta_0}$ too has a dramatic effect on the range, equally illustrated in Effigy 5(b). For a fixed initial speed, such equally might exist produced by a cannon, the maximum range is obtained with $\boldsymbol{\theta_0=45^o}.$ This is true only for weather condition neglecting air resistance. If air resistance is considered, the maximum angle is approximately $\boldsymbol{38^o}.$ Interestingly, for every initial bending except $\boldsymbol{45^o}$ there are 2 angles that give the aforementioned range—the sum of those angles is $\boldsymbol{90^o}.$ The range too depends on the value of the acceleration of gravity $\boldsymbol{g}.$ The lunar astronaut Alan Shepherd was able to drive a golf game ball a great altitude on the Moon considering gravity is weaker there. The range $\textbf{R}$ of a projectile on level ground for which air resistance is negligible is given by

$\boldsymbol{R\:=}$ $\boldsymbol{\frac{v_0^2\:\textbf{sin}\:2\theta_0}{g},}$

where $\boldsymbol{v_0}$ is the initial speed and $\boldsymbol{\theta_0}$ is the initial angle relative to the horizontal. The proof of this equation is left every bit an end-of-affiliate problem (hints are given), only information technology does fit the major features of projectile range as described.

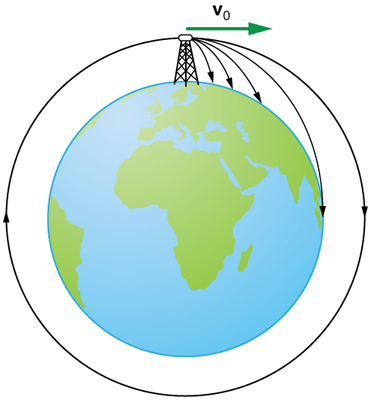
When we speak of the range of a projectile on level ground, we presume that $\textbf{R}$ is very small compared with the circumference of the World. If, however, the range is large, the Earth curves abroad below the projectile and dispatch of gravity changes direction forth the path. The range is larger than predicted past the range equation given above because the projectile has farther to autumn than it would on level ground. (See Effigy 6.) If the initial speed is swell enough, the projectile goes into orbit. This possibility was recognized centuries before it could exist achieved. When an object is in orbit, the Earth curves abroad from underneath the object at the aforementioned charge per unit as it falls. The object thus falls continuously merely never hits the surface. These and other aspects of orbital motility, such as the rotation of the Earth, will be covered analytically and in greater depth after in this text.

Once again nosotros see that thinking about 1 topic, such equally the range of a projectile, tin atomic number 82 us to others, such every bit the Earth orbits. In Chapter 3.5 Addition of Velocities, we will examine the improver of velocities, which is another important aspect of two-dimensional kinematics and volition likewise yield insights beyond the immediate topic.

A figure of the Earth is shown and on top of it a very high tower is placed. A projectile satellite is launched from this very high tower with initial velocity of v zero in the horizontal direction. Several trajectories are shown with increasing range. A circular trajectory is shown indicating the satellite achieved its orbit and it is revolving around the Earth.

PHET EXPLORATIONS: PROJECTILE Motion

Blast a Buick out of a cannon! Acquire about projectile movement by firing various objects. Set the angle, initial speed, and mass. Add air resistance. Brand a game out of this simulation by trying to hit a target.

Summary

Projectile motion is the motion of an object through the air that is subject area only to the acceleration of gravity.
To solve projectile motion bug, perform the post-obit steps:
1. Determine a coordinate system. So, resolve the position and/or velocity of the object in the horizontal and vertical components. The components of position $\textbf{s}$ are given by the quantities $\boldsymbol{x}$ and $\boldsymbol{y},$ and the components of the velocity $\textbf{v}$ are given by $\boldsymbol{v_x=v\:\textbf{cos}\:\theta}$ and $\boldsymbol{v_y=v\:\textbf{sin}\:\theta},$ where $\boldsymbol{v}$ is the magnitude of the velocity and $\boldsymbol{\theta}$ is its management.
2. Analyze the movement of the projectile in the horizontal management using the following equations:
  $\boldsymbol{\textbf{Horizontal motion}(a_x=0)}$
  
  $\boldsymbol{x=x_0+v_xt}$
  
  $\boldsymbol{v_x=v_{0x}=\textbf{v}_x=\textbf{velocity is a constant.}}$
3. Clarify the motion of the projectile in the vertical management using the post-obit equations:
  $\boldsymbol{\textbf{Vertical motion (Assuming positive direction is up;}\:a_y=-g=-9.80\textbf{ m/s}^2)}$
  
  $\boldsymbol{y=y_0\:+}$ $\boldsymbol{\frac{1}{2}}$ $\boldsymbol{(v_{0y}+v_y)t}$
  
  $\boldsymbol{v_y=v_{0y}-gt}$
  
  $\boldsymbol{y=y_0+v_{0y}t\:-}$ $\boldsymbol{\frac{1}{2}}$ $\:\boldsymbol{gt^2}$
  
  $\boldsymbol{v_y^2=v_{0y}^2-2g(y-y_0).}$
4. Recombine the horizontal and vertical components of location and/or velocity using the following equations:
  $\boldsymbol{s=\sqrt{x^2+y^2}}$
  
  $\boldsymbol{\theta=\textbf{tan}^{-1}(y/x)}$
  
  $\boldsymbol{v=\sqrt{v_x^2+v_y^2}}$
  
  $\boldsymbol{\theta_v=\textbf{tan}^{-1}(v_y\:/\:v_x).}$

Conceptual Questions

2: Reply the following questions for projectile motility on level ground assuming negligible air resistance (the initial angle beingness neither $\boldsymbol{0^0}$ nor $\boldsymbol{90^o}$ ): (a) Is the acceleration ever zero? (b) Is the acceleration ever in the same management as a component of velocity? (c) Is the dispatch ever reverse in direction to a component of velocity?

3: For a fixed initial speed, the range of a projectile is determined by the angle at which information technology is fired. For all but the maximum, there are 2 angles that requite the same range. Considering factors that might affect the ability of an archer to striking a target, such as air current, explain why the smaller angle (closer to the horizontal) is preferable. When would it be necessary for the archer to utilise the larger angle? Why does the punter in a football game use the higher trajectory?

iv: During a lecture demonstration, a professor places two coins on the edge of a tabular array. She then flicks ane of the coins horizontally off the table, simultaneously nudging the other over the edge. Describe the subsequent motion of the two coins, in particular discussing whether they hit the flooring at the aforementioned time.

Problems & Exercises

2: A ball is kicked with an initial velocity of sixteen m/south in the horizontal direction and 12 m/s in the vertical direction. (a) At what speed does the ball striking the ground? (b) For how long does the ball remain in the air? (c)What maximum height is attained by the brawl?

three: A brawl is thrown horizontally from the tiptop of a 60.0-1000 building and lands 100.0 thou from the base of the building. Ignore air resistance. (a) How long is the brawl in the air? (b) What must take been the initial horizontal component of the velocity? (c) What is the vertical component of the velocity merely before the ball hits the footing? (d) What is the velocity (including both the horizontal and vertical components) of the brawl just earlier it hits the ground?

4: (a) A daredevil is attempting to jump his motorbike over a line of buses parked finish to end past driving up a $\boldsymbol{32^0}$ ramp at a speed of $\boldsymbol{40.0\textbf{ m/s}\:(144\textbf{ km/h})}.$ How many buses tin can he clear if the top of the takeoff ramp is at the same height as the bus tops and the buses are xx.0 m long? (b) Talk over what your answer implies about the margin of error in this act—that is, consider how much greater the range is than the horizontal distance he must travel to miss the terminate of the final charabanc. (Neglect air resistance.)

5: An archer shoots an arrow at a 75.0 chiliad distant target; the bull's-heart of the target is at same acme as the release top of the pointer. (a) At what angle must the arrow be released to striking the bull'southward-eye if its initial speed is 35.0 thousand/s? In this role of the trouble, explicitly show how you follow the steps involved in solving projectile motility problems. (b) There is a large tree halfway between the archer and the target with an overhanging horizontal branch iii.50 grand in a higher place the release height of the arrow. Will the arrow get over or under the branch?

half dozen: A rugby player passes the ball 7.00 yard beyond the field, where information technology is caught at the aforementioned height as it left his hand. (a) At what angle was the brawl thrown if its initial speed was 12.0 m/south, assuming that the smaller of the two possible angles was used? (b) What other angle gives the same range, and why would it non be used? (c) How long did this pass take?

vii: Verify the ranges for the projectiles in Figure five(a) for $\boldsymbol{\theta=45^0}$ and the given initial velocities.

8: Verify the ranges shown for the projectiles in Figure 5(b) for an initial velocity of fifty m/southward at the given initial angles.

9: The cannon on a battleship tin can fire a trounce a maximum distance of 32.0 km. (a) Calculate the initial velocity of the shell. (b) What maximum elevation does it reach? (At its highest, the shell is above lx% of the atmosphere—just air resistance is not actually negligible as causeless to make this trouble easier.) (c) The ocean is non flat, because the Earth is curved. Assume that the radius of the Earth is $\boldsymbol{6.37\times10^3\textbf{ km}}.$ How many meters lower will its surface exist 32.0 km from the send along a horizontal line parallel to the surface at the ship? Does your respond imply that fault introduced by the assumption of a apartment Earth in projectile motility is significant hither?

10: An pointer is shot from a tiptop of ane.5 1000 toward a cliff of superlative $\textbf{H}.$ It is shot with a velocity of 30 grand/s at an angle of $\boldsymbol{60^0}$ above the horizontal. Information technology lands on the acme edge of the cliff iv.0 s later on. (a) What is the tiptop of the cliff? (b) What is the maximum meridian reached past the arrow along its trajectory? (c) What is the arrow's bear upon speed but before hitting the cliff?

11: In the standing broad jump, one squats and and then pushes off with the legs to meet how far one can jump. Suppose the extension of the legs from the crouch position is 0.600 m and the acceleration achieved from this position is 1.25 times the dispatch due to gravity, $\textbf{g}.$ How far can they jump? State your assumptions. (Increased range tin can be accomplished by swinging the arms in the direction of the jump.)

12: The world long spring record is 8.95 thou (Mike Powell, USA, 1991). Treated as a projectile, what is the maximum range obtainable by a person if he has a take-off speed of 9.5 m/s? State your assumptions.

xiii: Serving at a speed of 170 km/h, a tennis player hits the ball at a pinnacle of 2.5 m and an bending $\boldsymbol{\theta}$ below the horizontal. The service line is 11.ix 1000 from the net, which is 0.91 m high. What is the angle $\boldsymbol{\theta}$ such that the ball just crosses the net? Will the brawl country in the service box, whose out line is 6.xl m from the cyberspace?

14: A football quarterback is moving straight backward at a speed of ii.00 chiliad/s when he throws a pass to a player eighteen.0 m straight downfield. (a) If the ball is thrown at an angle of $\boldsymbol{25^0}$ relative to the ground and is caught at the same peak equally information technology is released, what is its initial speed relative to the ground? (b) How long does it accept to become to the receiver? (c) What is its maximum height above its bespeak of release?

xv: Gun sights are adjusted to aim loftier to compensate for the effect of gravity, effectively making the gun accurate only for a specific range. (a) If a gun is sighted to hit targets that are at the same height every bit the gun and 100.0 k away, how low will the bullet striking if aimed directly at a target 150.0 m away? The muzzle velocity of the bullet is 275 m/s. (b) Hash out qualitatively how a larger muzzle velocity would affect this problem and what would be the effect of air resistance.

xvi: An eagle is flying horizontally at a speed of iii.00 thousand/s when the fish in her talons wiggles loose and falls into the lake 5.00 grand below. Calculate the velocity of the fish relative to the water when it hits the h2o.

17: An owl is carrying a mouse to the chicks in its nest. Its position at that fourth dimension is 4.00 chiliad west and 12.0 grand above the center of the xxx.0 cm diameter nest. The owl is flight east at 3.50 chiliad/s at an bending $\boldsymbol{30.0^o}$ below the horizontal when information technology accidentally drops the mouse. Is the owl lucky enough to have the mouse hit the nest? To answer this question, calculate the horizontal position of the mouse when it has fallen 12.0 m.

eighteen: Suppose a soccer histrion kicks the brawl from a altitude 30 m toward the goal. Find the initial speed of the brawl if it just passes over the goal, 2.4 m above the footing, given the initial direction to be $\boldsymbol{40^0}$ above the horizontal.

19: Can a goalkeeper at her/ his goal kick a soccer ball into the opponent'due south goal without the ball touching the basis? The altitude will be well-nigh 95 m. A goalkeeper can give the ball a speed of 30 m/south.

20: The free throw line in basketball is 4.57 m (15 ft) from the basket, which is iii.05 m (10 ft) above the flooring. A role player standing on the free throw line throws the ball with an initial speed of 7.15 chiliad/s, releasing it at a pinnacle of two.44 k (viii ft) above the floor. At what angle above the horizontal must the brawl be thrown to exactly hit the handbasket? Note that most players will apply a large initial angle rather than a flat shot because it allows for a larger margin of fault. Explicitly testify how you follow the steps involved in solving projectile movement problems.

22: A basketball game player is running at $\boldsymbol{5.00\textbf{ m/s}}$ straight toward the basket when he jumps into the air to douse the ball. He maintains his horizontal velocity. (a) What vertical velocity does he need to rise 0.750 chiliad above the floor? (b) How far from the basket (measured in the horizontal direction) must he commencement his leap to reach his maximum superlative at the same time as he reaches the basket?

23: A football game player punts the brawl at a $\boldsymbol{45.0^0}$ angle. Without an outcome from the wind, the brawl would travel lx.0 m horizontally. (a) What is the initial speed of the ball? (b) When the brawl is near its maximum height it experiences a brief gust of wind that reduces its horizontal velocity by 1.fifty m/southward. What altitude does the brawl travel horizontally?

26: Unreasonable Results (a) Find the maximum range of a super cannon that has a muzzle velocity of 4.0 km/s. (b) What is unreasonable about the range you found? (c) Is the premise unreasonable or is the available equation inapplicable? Explain your respond. (d) If such a muzzle velocity could exist obtained, discuss the effects of air resistance, thinning air with altitude, and the curvature of the World on the range of the super cannon.

27: Construct Your Own Problem Consider a ball tossed over a fence. Construct a problem in which you calculate the ball's needed initial velocity to just articulate the argue. Amidst the things to determine are; the height of the fence, the distance to the fence from the point of release of the ball, and the elevation at which the brawl is released. Y'all should also consider whether it is possible to choose the initial speed for the ball and just calculate the angle at which it is thrown. Likewise examine the possibility of multiple solutions given the distances and heights you take called.

Glossary

air resistance: a frictional force that slows the motility of objects as they travel through the air; when solving basic physics problems, air resistance is assumed to be zero

kinematics: the study of motion without regard to mass or force

movement: deportation of an object equally a role of time

projectile: an object that travels through the air and experiences only dispatch due to gravity

projectile movement: the motion of an object that is subject only to the acceleration of gravity

range: the maximum horizontal distance that a projectile travels

trajectory: the path of a projectile through the air

Solutions

Problems & Exercises

$\boldsymbol{x=1.30\textbf{ m}\times10^2}$

$\boldsymbol{y=30.9\textbf{ m}.}$

iii:

(a) 3.50 s

(b) 28.6 m/s (c) 34.3 m/s

(d) 44.7 m/s, $\boldsymbol{50.2^0}$ below horizontal

five:

(a) $\boldsymbol{18.4^0}$

(b) The arrow volition go over the branch.

(a) 560 m/s

(b) $\boldsymbol{8.00 \times 10^3\textbf{ m}}$

11:

i.50 m, assuming launch angle of $\boldsymbol{45^0}$

13:

$\boldsymbol{\theta=6.1^0}$

yeah, the brawl lands at v.3 m from the internet

xv:

(a) −0.486 m

(b) The larger the muzzle velocity, the smaller the divergence in the vertical direction, because the time of flight would be smaller. Air resistance would have the consequence of decreasing the time of flight, therefore increasing the vertical departure.

17:

iv.23 m. No, the owl is not lucky; he misses the nest.

nineteen:

No, the maximum range (neglecting air resistance) is well-nigh 92 m.

21:

15.0 g/s

23:

(a) 24.2 m/due south

(b) The ball travels a full of 57.4 m with the brief gust of wind.

25:

$\boldsymbol{y-y_0=0=v_{0y}t-\frac{1}{2}gt^2=(v_0\:\textbf{sin}\:\theta)t-\frac{1}{2}gt^2},$